NODYCON2023 Keynotes

Periodic oscillations of multi-degree-of-freedom conservative systems were known to the earliest investigators of dynamics. It is now widely recognized that such motions are quite special. The Lyapunov subcenter theorem describes local invariant manifolds that contain families of such motions under certain non-resonance conditions. In seminal work in the 1960's, Rosenberg developed methods for describing and constructing these motions for conservative systems and labeled them as nonlinear normal modes (NNMs). Work on conservative systems was continued by Rand, Vakakis, Pak, and others through the 70's and 80's, including results on stability and bifurcations. In the early 90's the NNM concept was generalized by the presenter and Pierre to include non-conservative systems by employing invariant manifold theory. This approach spawned subsequent efforts on computational methods for generating reduced-order models using NNMs and experimental methods for capturing them, and also raised a fundamental question about the uniqueness of the underlying invariant manifolds, which has only recently been resolved. This talk will provide a survey of these developments, with a focus on my involvement with the subject.

Bio-sketch of Steven W. Shaw

Steve Shaw received his Ph.D. in Theoretical and Applied Mechanics from Cornell University in 1983. He currently is Professor of Mechanical Engineering at Florida Institute of Technology and University Distinguished Professor Emeritus of Mechanical Engineering and Adjunct Professor of Physics at Michigan State University. He has also held visiting appointments at Caltech, the University of Michigan, the University of California-Santa Barbara, and McGill University. His honors include the ASME Henry Hess Award, the SAE Arch T. Colwell Merit Award, the ASME N. O. Myklestad Award, the ASME T. K. Caughey Dynamics Medal, and election to the rank of Fellow of the ASME. His research has focused on nonlinear dynamics and vibrations with applications to piecewise smooth systems, nonlinear normal modes, vibration absorbers, and micro/nano-electro-mechanical systems.

I will split my talk into two parts:

1. First, I recall a few mathematical results for nonlinear dynamical systems (smooth or nonsmooth). The idea is to show that various mathematical tools could be useful to improve understanding of applied nonlinear dynamics. For nonsmooth systems, I will recall how numerical methods could be built from models involving maximal monotone operators in deterministic of stochastic frame without or with delay. I will also give a few examples of physical systems that could be treated by this approach or NLCP approach. For smooth systems, I will give a few examples to discuss advantages and limitations of algebraic tools (Groebner basis) used to obtain periodic solutions (in the frame of normal form theory or in the frame of analytical method applied to polynomial nonlinear dynamical systems to solve the problem of multiplicity of nonlinear periodic solutions).
2. Then I will recall the main ideas to develop nonlinear passive absorbers of Nonlinear Energy Sinks type and I will describe some results and applications of NESs. I will recall briefly how to design NESs and I will describe development of nonlinear passive control for different systems. For example:
   • a cable with horizontal or vertical oscillations
   • oscillations of a pendulum (cable car) attached to its cable
   • a nonlinear absorber to control essential tremor

Bio-sketch of Henri Lamarque

Claude Henri Lamarque received his Ph.D. in Mechanics at Ecole Centrale de Lyon in 1992 and Habilitation at Univ. Lyon in 1998. He received Engineer diploma from ENTPE and M.Sc. in Applied Mathematics from Univ. St-Etienne in 1985. He has been Head of Geo-Materials Laboratory (2002-2008) and Head of Building and Civil Engineering Department at ENTPE (2009-2012), Head of ENTPE's site of LTDS UMR 5513 CNRS (2012-2022), Head of GDR CNRS 3437 DYNOLIN (national research group in nonlinear dynamics of structures, 2011-2018). He is member of EUROMECH and ENOC Committee. He is currently Prof. at ENTPE (Univ. Lyon). His research is focused on nonlinear dynamical systems (smooth or nonsmooth), nonlinear vibrations and acoustics, applications to passive control of oscillations, reduced-order modeling, NEMS/MEMS, dynamics of cables, adaptive metamaterials. He has published over 180 archival publications, 2 patents, and 3 monographs.

This keynote discusses sensor design ideas developed in the context of networks of coupled linear and nonlinear oscillators of arbitrary topology. As an example, it presents a hysteretic sensor design, in which short bursts of exogenous excitation result in sustained endogenous network activity that returns to a quiescent state only after a characteristic time and along a different path than when originally excited. The desired behavior is obtained through the coupling of self-excited oscillations with purposely designed rate laws for slowly varying nodal parameters, governed only by local interactions in the network. The proposed architecture and the sought dynamics take inspiration from complex biological systems that combine endogenous energy sources with a paradigm for distributed sensing and information processing. As a second example, a hybrid realization of a mass sensor is presented, in which the dynamics of a physical cantilever are coupled asynchronously with a nonlinear oscillator realized in a simulation model. An iterative algorithm ensures that the dynamics in the asymptotic limit mimics self-excited oscillations of a nonlinear oscillator network, while eliminating any effects of distortion from actuator latency. The use of parameter continuation techniques in the associated bifurcation analysis and design validation is illustrated using the open-source package coco.

Bio-sketch of Harry Dankowicz

Harry Dankowicz is Professor of Mechanical Science and Engineering in The Grainger College of Engineering at the University of Illinois at Urbana-Champaign. He graduated from KTH Royal Institute of Technology in Stockholm, Sweden, with an M.Sc. in Engineering Physics in 1991 and from Cornell University with a Ph.D. in Theoretical and Applied Mechanics in 1995. Following postdoctoral and research associate appointments at KTH between 1995 and 1999, he joined the Department of Engineering Science and Mechanics at Virginia Polytechnic Institute and State University, where he remained until 2005. Since May 2021, he is Program Director for the Dynamics, Control and Systems Diagnostics Program in the Division of Civil, Mechanical and Manufacturing Innovation at the National Science Foundation. Prof. Dankowicz is a recipient of a Junior Investigator Grant from the Swedish Foundation for Strategic Research and CAREER and PECASE awards from the US National Science Foundation, a Fellow of the ASME, and a recipient of the Fred Merryfield Design Award and Archie Higdon Distinguished Educator Award from the ASEE. In fall 2022, he concluded a ten-year term as Editor-in-Chief of ASME Applied Mechanics Reviews.

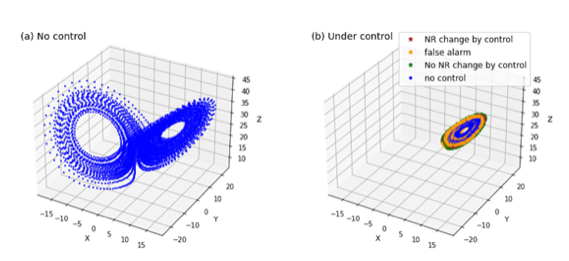
The Observing Systems Simulation Experiment (OSSE) is a very powerful approach to evaluate observing systems and data assimilation methods in numerical weather prediction (NWP). In the OSSE, we generate a nature run (NR) using a model and simulate observations by sampling the NR. An independent model run with data assimilation of the simulated observations mimics an NWP system, and we compare it with the NR to evaluate the observations and data assimilation method. In this study, we extend the OSSE and design the Control Simulation Experiment (CSE), in which we add perturbations to the NR and try to modify it to a desired state. Investigating what perturbations are effective to avoid a high-impact weather event would be useful to understand the controllability of such an event. Since the weather system is chaotic, and even more so for disturbances, small differences generally lead to big differences, particularly for high-impact weather events. This suggests potentially effective control, i.e., small interventions would lead to big differences for high-impact weather events. Chaos control has been studied extensively in the field of dynamical systems theory, but taking advantage of dynamical instability to avoid certain trajectories has not been a main focus to the best of the authors' knowledge. We first tested this idea with the Lorenz-63 3-variable model and performed an OSSE with an ensemble Kalman filter (EnKF). We extended the OSSE by adding very small perturbations (only 3% of the observation error) to the NR and found an effective approach to control the trajectory to stay in one side of the Lorenz's butterfly attractor without shifting to the other. Following the implications and understandings from the Lorenz-63 model experiments, we tested with the Lorenz-96 40-variable model to avoid the occurrences of extreme values, mimicking to avoid extreme events in NWP. Finally, we further extended the idea to test with realistic global and regional NWP models for a typhoon case and a local heavy rainfall case, respectively. This presentation will summarize the concept and methodology of CSE with some proof-of-concept demonstrations with the toy models and realistic NWP models. This is an attempt to a potential paradigm change of NWP research from decades of predictability to the new era of controllability.

Bio-sketch of Takemasa Miyoshi

Dr. Takemasa Miyoshi received his B.S. (2000) in theoretical physics on nonlinear dynamics from Kyoto University, and M.S. (2004) and Ph.D. (2005) in meteorology on ensemble data assimilation from the University of Maryland (UMD). Dr. Takemasa Miyoshi started his professional career as a civil servant at the Japan Meteorological Agency (JMA) in 2000. He was a tenure-track Assistant Professor at UMD in 2011. Since 2012 Dr. Miyoshi has been leading the Data Assimilation Research Team in RIKEN Center for Computational Science (R-CCS) and became Chief Scientist of RIKEN Cluster for Pioneering Research (CPR) and Deputy Director of RIKEN interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS) in 2018. Dr. Miyoshi's scientific achievements include more than 140 peer-reviewed publications and more than 180 invited conference presentations including the Core Science Keynote at the American Meteorological Society Annual Meeting (2015). Dr. Miyoshi has been recognized by several prestigious awards such as the Japan Geosciences Union Nishida Prize (2015), the Meteorological Society of Japan Award (2016), the Yomiuri Gold Medal Prize (2018), the Commendation by the Prime Minister for Disaster Prevention (2020), and the Award for Science and Technology by the Minister of Education, Culture, Sports, Science and Technology (2022).

Flow control is a many-decades old engineering problem of a multi-disciplinary nature. It is concerned with devising passive or active means of intervention with the flow structure and its underlying mechanisms in a manner that causes desirable changes in the overall flow behaviour. For streamlined bodies cruising through a flow, such as air or water, there is a key interest in the control of flow instabilities which manifest as fluid waves. These are disturbances or fluctuations in the flow velocity field that if left to grow are likely to trigger transition of the flow from laminar to turbulent, which in turn causes significant increases in skin-friction drag. A rise in drag reduces the fuel efficiency in aircrafts and 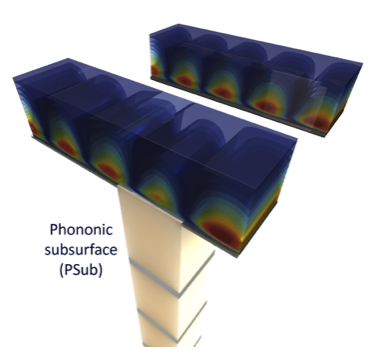ships. It is therefore desired to device intervention methods to impede the growth of these instabilities. Alternatively, in some scenarios, the objective may be to speed up the growth of the instabilities and laminar-to-turbulent transition to prevent or delay flow separation. In recent research, we have shown that phonon motion underneath a surface interacting with a flow may be tuned to cause the flow to stabilize, or destabilize, as desired [Hussein et al., Proc. R. Soc. A, 2015]. The underlying control mechanism utilizes core concepts from crystal physics, primarily, the principle of destructive or constructive interferences and the notion of symmetry breaking. This is realized by installing a “phononic subsurface” (PSub), which is an architectured structure placed in the subsurface region and configured to extend all the way such that its edge is exposed to the flow, forming an elastic fluid-structure interface. The PSub may take the form of a phononic crystal or an elastic metamaterial, with finite extent, and is typically oriented perpendicular to the fluid-structure interface. It is engineered to exhibit specific frequency-dependent amplitude and phase response characteristics at the edge exposed to the flow. By simulating the 3D nonlinear Navier-Stokes equations, we will present results demonstrating perfectly synchronized passive phased response and energy exchange between the elastic domain of a PSub and the perturbation (instability) field within an interfacing flow. As an example, a flow in a channel retrofitted with a PSub underneath the channel walls will be considered. These results suggest a new paradigm in flow control based exclusively on principles from phononics.

Bio-sketch of Mahmoud I. Hussein

Mahmoud I. Hussein is the Alvah and Harriet Hovlid Professor at the Smead Department of Aerospace Engineering Sciences at the University of Colorado Boulder. He holds a courtesy faculty appointment in the Department of Physics and an affiliate faculty appointment in the Department of Applied Mathematics, and he has formally served as the Engineering Faculty Director of the Pre-Engineering Program and the Program of Exploratory Studies. He received a BS degree from the American University in Cairo (1994) and MS degrees from Imperial College London (1995) and the University of Michigan-Ann Arbor (1999, 2002). In 2004, he received a PhD degree from the University of Michigan-Ann Arbor, after which he spent two years at the University of Cambridge as a postdoctoral research associate.

Dr. Hussein's research focuses on the dynamics of materials and structures, especially phononic crystals and metamaterials, at both the continuum and atomistic scales. His research considers areas that range from vibrations and acoustics of engineering materials and structures and passive flow control to lattice dynamics and thermal transport in semiconductor-based nanostructured materials. His studies are concerned with physical phenomena governing these systems, associated theoretical and computational treatments, and analysis of relevant mechanisms such as dispersion, resonance, dissipation, and nonlinearity. His team also conducts experiments to support some aspects of the theoretical work. Dr. Hussein received a DARPA Young Faculty Award in 2011, an NSF CAREER award in 2013, and in 2017 was honored with a Provost's Faculty Achievement Award for Tenured Faculty at CU Boulder. He has co-edited a book titled Dynamics of Lattice Materials published by Wiley. He is a Fellow of ASME and has served as an associate editor for the ASME Journal of Vibration and Acoustics. In addition, he is the founding vice president of the International Phononics Society and has co-established the Phononics 20xx conference series which is widely viewed as the world's premier event in the emerging field of phononics.